4021. Knight move

The rectangular board of size n × m (n rows and m columns) is given. The chess knight is located in the left upper corner. You must relocate it to the right lower corner. The knight can move only either two cells down and one right, or one cell down and two cells right.

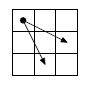
Find the number of knight paths from the left upper corner to the right lower corner.

Input. Two positive integers n and m (1 ≤ n, m ≤ 50).

Output. Print the number of ways to relocate the knight from the left upper corner to the right lower corner of the board.

Sample input 1	Sample output 1
3 2	1
Sample input 2	Sample output 2
31 34	293930

SOLUTION

dynamic programming

Algorithm analysis

Let dp[i][j] contains the number of ways to run from left upper corner – the cell with coordinates (1, 1) into right lower corner – the cell with coordinates (n, m). Assign zeroes to array dp and set dp[1][1] = 1.

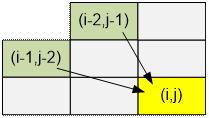
According to the knight moves, we can come into cell (i, j) only either from (i – 1, j – 2) or from (i – 2, j – 1). So

dp[i][j] = dp[i – 1][j – 2] + dp[i – 2][j – 1]

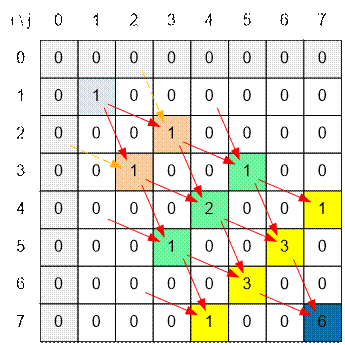
Sample

Fill the array dp for the board of size 7 * 7:

Algorithm realization

Declare two dimensional array.

#define MAX 55

int dp[MAX][MAX];

Read the input data.

scanf("%d %d",&n,&m);

Calculate the values for elements of array dp. Since the knight can not get into the cells of the first row and the first column (except the initial position), then the loops by i and by j can be started from 2.

memset(dp,0,sizeof(dp));

dp[1][1] = 1;

for (i = 2; i <= n; i++)

for (j = 2; j <= m; j++)

dp[i][j] = dp[i-1][j-2] + dp[i-2][j-1];

Print the answer.

printf("%d\n",dp[n][m]);

Java realization

import java.util.*;

public class Main

{

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

int m = con.nextInt();

long dp[][] = new long [n+1][m+1];

dp[1][1] = 1;

for (int i = 2; i <= n; i++)

for (int j = 2; j <= m;j ++)

dp[i][j] = dp[i-1][j-2] + dp[i-2][j-1];

System.out.println(dp[n][m]);

con.close();

}

}